Executive Summary:

I developed a process for cleaning and validating historical data (specifically World War Two bombing data in this example), for which machine learning techniques are not readily appropriate as error is indeterminable with no available training labels. I transformed the data from being prohibitively inconsistent and dirty to only showing few and subtle errors in geospatial information using a carefully constructed data cleaning pipeline and a new and quick way of forming classification decision boundaries I developed for this project.

 

Motivations:

As might be expected for decades-old government records, the geospatial data I had in my hands for my Shiny project was prohibitively messy for graphing outright (e.g., with European cities showing up in Africa and Asia, among other similar issues) and needed to be thoroughly cleaned. The slight redundancy of the data (consisting of a city, a country, a latitude, and a longitude) offered hope of this despite significant missingness and outright errors. Below I outline the approach I took for cleaning the data, specifically data for World War Two, as it needed the greatest extent of cleaning.

 

Examples:

 

This slideshow requires JavaScript.

There were many kinds of errors, the most prominent of which were cities obviously belonging to one country appearing associated with another real country (in an relatively unpatterned manner) and apparent OCR (optical character recognition) or data-entry mistakes, which I presume to be responsible for the frequent misspellings of cities and errors in recorded latitudes and longitudes.

 

Cleaning of such data from a recent (non-historical) context would be easier, as one can simply use Google’s Maps API to check city and country of each latitude-longitude pair (no machine learning or machine learning approximations necessary). For one, however, such approaches cost money for more than a small volume of API calls, prohibiting me from using them to validate my hundreds of thousands to millions of rows of data. More fundamentally, however, is the problem of historical changes: Yugoslavia (for example) no longer exists, and even if its shadow is still fairly recognizable on modern maps as a composite of descendant countries, many borders themselves have changed since the World War Two era, making such external validation less valuable. Instead, I developed a method of sufficiently cleaning and validating the data internally by carefully making select edits in the data pipeline in a methodical order and with a new (and quick) decision boundary formation technique.

 

In order to optimally clean this data, I had to consider the contingencies of fixing each kind of data error on fixing (or potentially introducing) further errors of other types. I’ll outline the rough logic for my resulting solution below, but first, the order:

 

1. Discover and fix incompletely-named cities
2. Reassign city and/or country values for minority data clustered at the same location as other similar data with different city and/or country values
3. Discover and fix off-by-integer errors in latitude and longitude for each city
4. Find cities with high variation in their latitude and/or longitude values and reassign city/country values if those coordinates better matched other cities
5. Fill in missing country values for cities that already agree on coordinates
6. Make each coordinate fix its country by predicting which country it should be in based on its coordinates and the sizes of the countries:
   1. Leaving the country value as is if it’s at least rank 2 in confidence and reasonably close
   2. Updating the country value to the top prediction otherwise
7. Filling in missing country values by city
8. Filling in missing country values by coordinate
9. Fix city spellings based on string distances
10. Fill in missing city values by coordinate
11. Mean-impute coordinates by city

 

City values were important to fix earlier on, as they relate closely to both coordinates (being closely clustered geospatially) and to country (usually having a unique name within the overall namespace of cities and uniquely mapping to a country), so I picked off the low-hanging fruit of incomplete city names first to ensure that more relevant data were available to fix coordinates and countries. I only fixed incomplete city names as opposed to similar misspellings because the checking for misspellings was prohibitively computationally expensive without first segmenting by country (and at this point, there were still many errors in the country values). (By this point in the data cleaning process, all country misspellings had already been fixed with my replace_levels function, as the number of countries was feasibly low enough to handle manually.)

 

Another quick fix of errors of relatively high confidence is allowing majority-rule voting for the correct country and city values for data all at the same coordinates.

 

With cities more reasonably linked to coordinates at this point, it was possible to search through each city for off-by-integer data-entry errors in the latitude and/or longitude coordinates (as no city occupies even close to one degree of latitude’s or longitude’s worth of space, and such single-digit mistakes were common).

 

After fixing data entry errors on coordinates, it was possible to fix data entry errors on city/country values by sifting through cities with high variance in either coordinate and detecting matches to other existing cities.

 

Before we use country value information, it helps to fill in what data we can there, so coordinates linked to one and only one country were filled to all link to that country.

 

Finally, on to the decision boundary metric:

I predicted which country’s territory a location existed in by measuring the Euclidian distances to country centroids normalized by country size. I first generated the centroid locations by averaging existing latitude-longitude pairs for each country (finding the country’s center of mass) and then tweaking it manually as I identified mistakes.

 

Importantly, it’s unreasonable to assume that each coordinate simply belongs to the country it’s geographically closest to (using the non-normalized Euclidian distance), as in that case much of western Germany’s and northern France’s territory would look like it belongs to tiny Luxembourg. Instead, when relative country territory sizes are taken into account, the decision boundaries that form roughly approximate the map even without explicitly modeling country territories as disks in the plane. For example, a location 200km away from a 2x-size country’s center and 100km away from a 1x-size country’s center would rightly be predicted to lie on the border. Some countries are very much non-circular (take Austria or Italy as example); such countries were composed of a few smaller model centers (each classifying to the same country) that better approximate the overall territory shape. This allowed fairly good internal validation of country value in a nearly automatic fashion (with only a few tweaks, such as manually breaking down non-circular countries appropriately, though in hindsight I probably could have automated that too). I had considered training one-against-all radial SVMs as a way to provide adequate separation, though since the errors were already baked into the training data (some to a terrible degree), this seemed like a poor idea and I went with this new size-normalized distance metric instead. Similarly, K-Nearest Neighbors would have failed given the very uneven distribution (both spatially and in number) of data on either side of known borders in addition to the dirtiness of the training data.

 

Such a distance metric turns out to have some interesting properties. For instance, for two territories, the decision boundary also turns out to be a circle (enclosing the smaller territory, though not necessary with it at its center) with a diameter given by 2abd/(b^2 – a^2), where a and b are the sizes of the two territories in question and d is the distance between these two territories’ centers. For territories of the same size, this means that a circle of infinite radius (effectively a straight line bisecting the segment from one territory’s center to the other’s, which makes sense) forms the decision boundary, essentially just assigning points in the plane to the country closest to it in the ordinary Euclidian sense. For territories similar but not equal in size, the decision boundary circle is centered very far from the smaller territory’s center (which is near the decision boundary itself), such that it loosely approximates the bisecting line decision boundary of equally sized territories, and for territories dissimilar in size, the decision boundary circle is centered very close to the smaller territory’s center (the smaller territory appears as an enclave within the larger territory). Things get more complicated when more than two territories enter the picture, but you can see how an evenly-spaced grid of longitudinal and latitudinal points are assigned to countries in Europe below. The assignments are accurate enough to correct most errors in country assignment despite coming from a model with not that many more degrees of freedom than prediction classes and no machine learning optimization of the parameters (each region has a center and a size for a total of three degrees of freedom per region, though in effect I mostly only quickly tweaked the sizes).

 

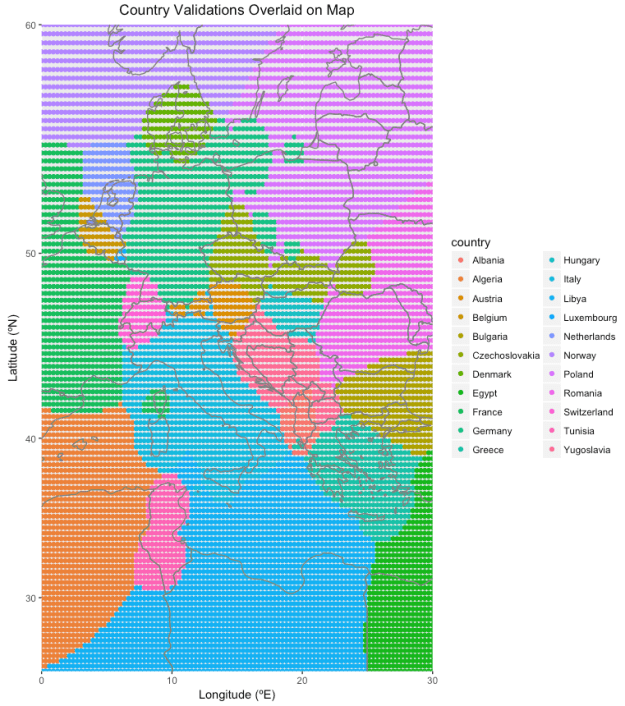
Again, the sloppiness of the decision boundaries is mitigated by only forcing the data to change their country assignments if the country they’re assigned to is ranked sufficiently poorly in predicted likeliness. I also did not spend any time tweaking non-contentious borders (such as Libya-Algeria).

 

After all aspects of the data had been cleaned, I was then able to confidently segment the data by country (trusting that all misspellings of each city are mapped inside a single country) to avoid the O(N^2) explosion of computation time for generating string distances for a vector of N strings, and fix spelling errors in city value. Having the most accurate city and coordinate information, I finally imputed missing coordinates using mean imputation based on city.

 

The final product shows good separation of data by country (though keep in mind that many borders, such as the Sudetenland and Alsace-Lorraine, were different back then, and many imperial colonies had not yet gained independence).